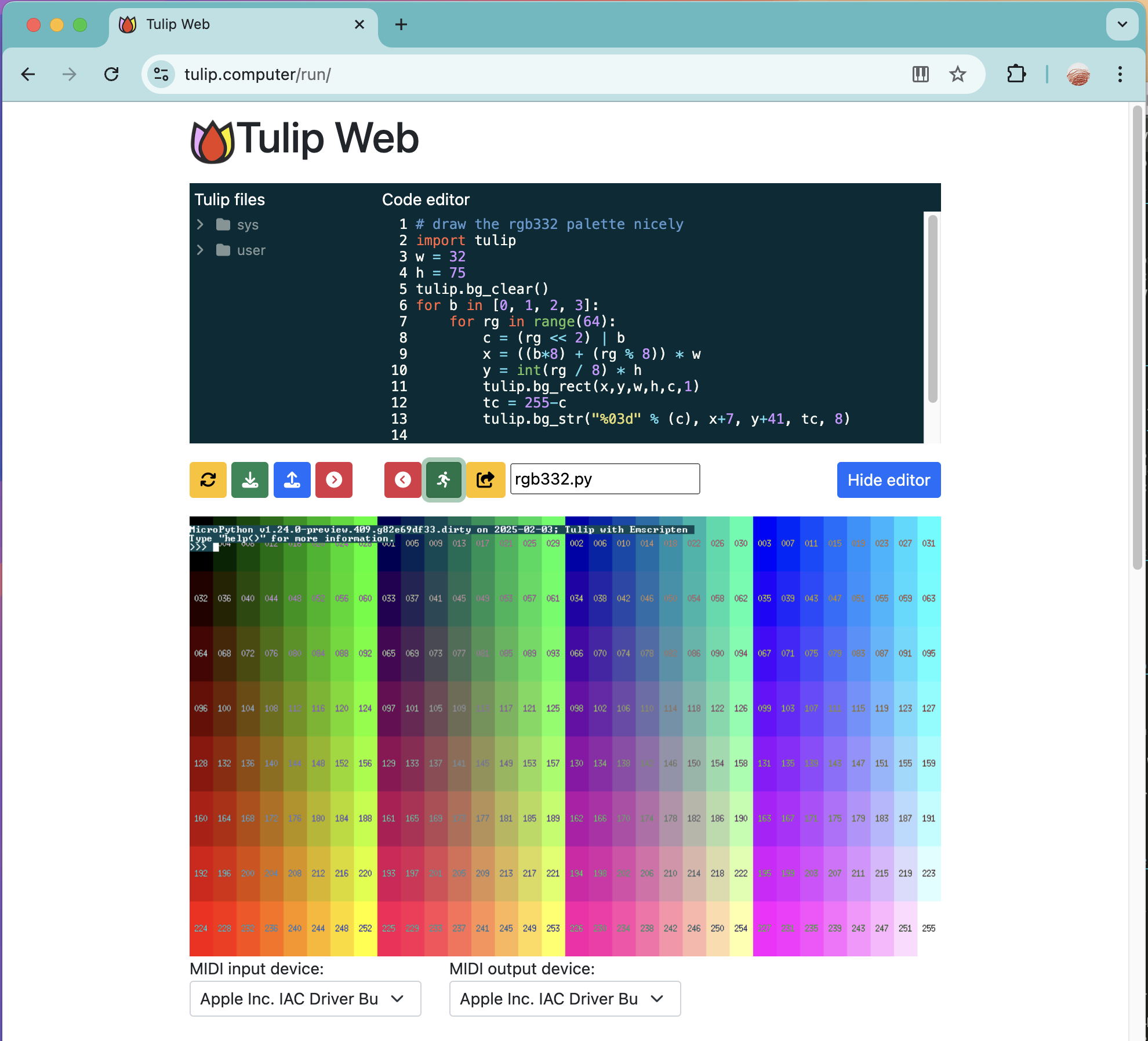
Just over one hundred years ago, the British carried out one of the most audacious acts in the history of codebreaking. So audacious, in fact, that they had to convince the Americans they hadn’t done it at all…
The Admiralty
Running, Lieutenant Nigel De Grey decided as he narrowly avoided colliding with another paper-laden trolley, was not something that the corridors of the Admiralty Old Building had been designed for.
Nor was it something that the Royal Navy approved of from its junior officers, apparently. This was clear from the angry shouts of the people he dodged as he raced down the building’s narrow back corridors.
Right now though De Grey didn’t care. It was 17th January 1917 and Europe had been locked in a bloody stalemate for almost three years, but the scrap of paper he held in his hand might well change the outcome of the Great War.
The dormouse
Although he now spent his days in London, was more than familiar with the horrors happening on the Western Front. The son of a reverend, De Grey had worked at a publishing company before the war where he’d been nicknamed “dormouse” by his colleagues due to his shyness. At the same time he had been a member of the Royal Naval Reserve. He was called up early and, as a result, had been in combat in Belgium during the early days of the war.
In 1915, however, De Grey’s fluency in both German and French, his quick mind and his love of a good puzzle had been noticed by the powers that be. Without warning, he was ordered back to London to join a mysterious Naval department known as ‘Room 40.’
The Room
Room 40 had only existed for a few short months when De Grey joined, although plans had existed for such an organisation should war break out since 1911. That it existed at all was because the world of warfare — or more importantly the way that people communicated in war — was changing. Radio, telegraph and telephony were now viable forms of communication, and so were also potentially vital sources of intelligence too. The arrival of war brought with it a myriad of opportunities for such intelligence gathering. In August 1914, for example, a Russian attaché gave the Admiralty a copy of a German codebook taken from the beached German cruiser SS Magdeburg. In a spare room (you can guess the number) at the back of the old Admiralty building, a small group of officers and civilians were given a new job — break and read German communications. De Grey joined soon after. It was here that he discovered what he would later describe as his ‘higher calling’ — he became a codebreaker.
The Research Group
In fact, De Grey was soon assigned to an even smaller, more mysterious team within Room 40 — the ‘Research Group’. A secret department within a secret department, its innocuous name was cover for work which was anything but. For whilst trying to read your enemy’s message traffic was considered acceptable (if unsporting) behaviour during wartime, doing the same thing to neutral powers was seriously frowned upon. Yet this was exactly what the Research Group had been created to do.
That such an opportunity existed was due to the way transatlantic communication worked at the time. Radio was getting more advanced and powerful, but it was not yet good enough to provide worldwide coverage. This meant that most diplomatic traffic still circulated in telegraph form, sent across vast distances by cable.
For the Entente powers in the First World War this wasn’t really a problem. Britain and France were both at the height of their imperial power and their telegraph networks spanned the globe. Germany, however, did not have that luxury. Its cables — particularly those stretching across the Atlantic — lay well outside its zone of military control.
This situation was not lost on the Entente. Almost as soon as war was declared, much of Germany’s overseas cable network went dark. It didn’t take an expert to know why — the Royal Navy had cut most of the cables, and Germany realised those that which remained suspiciously uncut should probably be considered compromised.
The Neutral
Robbed of the ability to communicate with their embassies throughout the world, the Germans protested. They complained that this was as an outrageous violation of diplomatic protocol — even during war.
Unsurprisingly, their complaints fell on deaf ears within the Entente itself. Luckily for the Germans, however, there was one major power who agreed with them — the United States of America. America was staunchly neutral at the time, the only ‘great power’ not involved in the war and its President, Woodrow Wilson, believed that if the the US were to have any hope of mediating an end to the war in Europe, then German diplomats in the US and beyond needed to be able to talk freely to their government.
It was a noble goal, and so to further it the US State Department granted Germany permission to use the American transatlantic cable, via Copenhagen, for diplomatic telegraph traffic.
Both Germany and the US believed these messages to be entirely secure. German intelligence had sufficiently penetrated the State Department to know that the Americans weren’t interested in breaking Germany’s codes. More importantly though, both powers believed that the British would not tap into US traffic — to do so would cause an enormous diplomatic incident. Not that it mattered anyway — even if they were tempted, the Germans thought they were safe. They understood that the US cable was entirely submarine, and thus safe from tampering.
The Germans were right on the first account, Unfortunately were wrong on both the latter.
The interception
Whatever the thoughts of the British Foreign Office might be, the Admiralty had its own opinions on what was, and wasn’t, fair game when it came to intelligence gathering. If the Americans were going to transmit coded German messages for them, then as far as Captain Reginald “Blinker” Hall, the Director of Naval Intelligence and ultimate head of Room 40 was concerned, American diplomatic traffic was absolutely fair game.
Again, had the Germans been correct about the American submarine cable then this still wouldn’t have been a problem, but they weren’t. In fact, US telegraph traffic came ashore on Britain via a relay station just north of Newcastle and then travelled across the country to Cornwall. From there it was then transmitted onward to Washington. This presented multiple opportunities for the messages to be intercepted by the British, and the Research Group was born. Every day they would receive copies of the traffic sent across the line. Their job was to crack the codes and read every diplomatic message the Americans and the Germans sent.
It was a decrypt of one of those diplomatic messages that De Grey now clutched in his hand as he raced down the Admiralty’s narrow oak halls. Sent the night before, it was pure luck that it had been decrypted so quickly. It was only a short message, which had been sent by Arthur Zimmermann, the German Foreign Minister, to the German ambassador in Mexico. As such, it was considered low-level diplomatic traffic and had been marked as low-priority for breaking and decryption. By chance, however, when it had arrived at Room 40 the pneumatic Tube system had dumped it on the desk of one of the department’s other rising stars, Alfred Dillwyn Knox.
The genius
A Classics scholar and papyrologist at Cambridge before the war, “Dilly” had joined Room 40 in 1914. There he swiftly demonstrated an unquestionable genius for codebreaking. Indeed Dilly Knox remains one of the greatest codebreakers Britain has ever produced. After the end of the First World War, he would become one of the founding fathers of the Government Code and Cypher School — GCHQ, which remains Britain’s primary cryptographic line of defence to this day. Nor does his influence end there. In 1925 in Vienna, he became the first British Intelligence officer to acquire an Enigma machine. Then in Warsaw, in 1938, it was to Dilly that the Poles were prepared to turnover their own Enigma codebreaking efforts. It was also Dilly who oversaw the transfer of that information — and a number of Polish codebreakers who managed to escape the Nazi invasion of Poland — to a new codebreaking institution he had helped set up back in Britain — Bletchley Park.
What many people don’t realise is that ‘Enigma’ wasn’t one code — it was many. The most complex of these (thanks to an extra rotor on the machine) was the German Naval code. The honour for breaking that rightly belongs to Alan Turing, but he was not the only man working on Enigmas. Dilly himself broke not one, but three of the other key codes — those of Spanish Intelligence, the German Army and the Italian Navy. To take full advantage of these, he then fought for the right to form a unique codebreaking outfit at Bletchley — “Intelligence Service Knox” (ISK). Under Knox, ISK became the only codebreaking department at Bletchley entirely staffed by women.
The ‘Dilly Girls’
Dilly had spotted that whilst women were considered a vital cog in the Bletchley codebreaking machine, they were almost exclusively confined to ‘support’ roles — Bombe operators, transcribers, translators and beyond. Dilly saw this as a waste of good minds, based solely on flawed preconceptions about gender, at a time when Britain needed good minds the most.
The formation of ISK was not without controversy. Rumours soon circulated that Dilly had wandered round the huts pointing at the prettiest girls for his ‘eastern harem’, and they were soon being referred to by the derogatory nickname ‘Dilly’s Girls’.
Nothing could have been further from the truth. Once permission had been given to form ISK, Dilly had immediately approached the head of the Women’s section, who interviewed all of the female staff sent to Bletchley and managed them once they’d arrived. He asked her to reassign those she considered most wasted in their current roles to ISK and the results soon spoke for themselves. ISK became one of the most successful codebreaking teams at Bletchley, contributing critical decryptions that would help win the naval war in the Mediterranean and ensure the success of the D-Day landings. Indeed ISK’s contributions outlived Dilly himself (who died suddenly of cancer in 1943), with the department proudly adopting and subverting the ‘Dilly’s Girls’ moniker until the end of the war.
The revelation
In 1917, of course, all this was in the future. Right now Dilly’s efforts were focused firmly on finding new ways into German naval codes. Unusually, Dilly was not particularly mathematical. What he was good at, however, was spotting patterns and looking at things from unusual angles, in part the result of his experience rebuilding and translating Greek manuscripts from mere fragments before the war. He also had a near-uncanny ability to put himself in the mind of the people at the other end of the line. In 1915 he had broken the German Admiralty’s flag code by spotting — and exploiting — one particular German telegraph operator’s love of romantic poetry. These efforts had put Dilly on the Research Group’s radar, and though he was not officially a member of the team he had been quietly called in to help with their work from time to time.
Indeed this was perhaps why this particular intercept had dropped from the Admiralty’s pneumatic tube system onto Dilly’s desk on the night of the 16th January. With the rest of the Research Group busy that night, it might have been that Dilly was seen as an overflow for the low-level traffic. Whatever the reason, something about this particular message caught Dilly’s eye. Rather than leaving it at the bottom of his pile, he worked on trying to break it right through the night.
By morning, he had begun to make inroads into the telegram. Dilly didn’t speak German, but he recognised words such as “Submarine”, “Mexico” and “Arizona”. He became increasingly convinced that the telegram was important and so, when De Grey arrived at work the next morning, Dilly roped him in to help. The two men had worked as a decryption team before with considerable success — De Grey’s fluent German and experience as an editor meshing well with Dilly’s own skills. Together they worked on the telegram right through the morning. The more they decrypted, the more both men became astonished at what they were reading — indeed they could barely believe it. By lunchtime, however, they had decrypted enough to know that they weren’t wrong. They agreed the Captain needed to see this immediately.
Normally athletics wouldn’t have been necessary. Officially, everyone in Room 40 reported to Sir Alfred Ewing, who himself then reported to “Blinker” Hall. Sometime before, however, the Captain himself had quietly pulled De Grey and the other men of the Research Group aside. Ewing, Hall told them, was a bit of a chatterbox in the corridors of power and Hall didn’t trust him to keep a really big secret. If the Research Group’s work ever yielded something particularly sensitive or explosive, then they were ordered to bypass Ewing completely and only reveal what they had found to Hall himself. So this was where De Grey was headed.
The Captain
De Grey entered the Captain’s outer office at a sprint, bursting into the Hall’s office before his personal secretary could object. Luckily, the Captain was in.
“Do you want to bring America into the war sir?” De Grey burst out breathlessly.
“Yes, why?” Replied the slightly bemused Hall. He had long since stopped expecting any semblance of military decorum or normality from his codebreakers.
“I’ve got a telegram that will bring them in if you give it to them.” De Grey blurted out, thrusting the results of his own and Dilly’s efforts towards the Captain.
Hall took the decrypt and read it, silently, as De Grey explained who it was from, for and how they had broken it. For the very first time, a senior member of British Intelligence held in his hands a copy of what would become known to history as the ‘Zimmermann Telegram.’
We intend to begin on the first of February unrestricted submarine warfare. We shall endeavour in spite of this to keep the United States of America neutral. In the event of this not succeeding, we make Mexico a proposal of alliance on the following basis: make war together, make peace together, generous financial support and an understanding on our part that Mexico is to reconquer the lost territory in Texas, New Mexico, and Arizona. The settlement in detail is left to you. You will inform the President of the above most secretly as soon as the outbreak of war with the United States of America is certain and add the suggestion that he should, on his own initiative, invite Japan to immediate adherence and at the same time mediate between Japan and ourselves. Please call the President’s attention to the fact that the ruthless employment of our submarines now offers the prospect of compelling England in a few months to make peace.
Signed, ZIMMERMANN
The telegram
Hall listened patiently as De Grey outlined both what they new for certain and what were guesses at length. By the time De Grey had finished, Hall was happy to accept what he was saying was true. At this stage, they had not fully decrypted the message (the above is the full, final text), but it was more than enough for Captain Hall to grasp that De Grey wasn’t exaggerating. This wasn’t just confirmation that Germany were preparing to conduct unrestricted submarine warfare — it was incitement to Mexico to declare war on the United States.
Whilst Zimmermann has been cast in history as something of a naive operator, the truth is anything but. Zimmermann was one of the architects of Germany’s successful policy of funnelling money and support to rebellions and rivals of the Entente powers. This had caused enormous problems for them, forcing them to spread their forces thinner across the world. Indeed at that very moment this approach was yielding enormous results in Russia, who would be forced out of the war entirely before the year was out.
Get John Bull’s stories in your inbox
Join Medium for free to get updates from this writer.
Zimmermann’s telegram was intended to lay the groundwork for the same approach to be taken across the Atlantic, in the event that the declaration of unrestricted submarine warfare be enough to tip the balance of US government into intervening.
Not only were the Germans suggesting Mexico declare war on the United States (with German backing) but, even more incredibly, they were using the using US State Department’s own telegraph network to do it.
The problem
If unrestricted submarine warfare itself didn’t drag the US into the war, then Hall realised that De Grey and Dilly were right — this telegram (and the outrageous way it had been sent) could well be enough to do so.
Hall, however, was fully aware that he had a problem. Indeed the mother of all intelligence problems. One of the regular problems with good intelligence was working out how to use it without ‘burning’ the source — because revealing it might inadvertently reveal to the enemy how you got it, cutting you off from all future intelligence by the same method.
Hall’s problem here was even worse. Not only would revealing the existence of the telegram burn the source, as the Germans would know the US cable was compromised, but that source was, effectively, the US State Department itself.
“Hello chaps, we’ve been reading your mail, and there’s some things in here you really should see…” Was a line that was hardly likely to go over well with the Americans. Indeed they may be more than outraged enough about that to eclipse any horror at the telegram itself.
Hall’s solution
Recognising the explosiveness of the situation, Hall and De Grey briefly discussed their options. Realising that whatever he did, he should probably lock things down until they had a plan.
Claude Serocold, Hall’s personal assistant was inducted into the secret and the men then pitched around more ideas as to how they could get the telegram into the hands of the Americans without blowing the source. In the end, it was Hall himself who had the brainwave that led to the solution.
Looking at the intercept, he realised that although the final destination of the telegram was the German Ambassador in Mexico, it hadn’t been sent to him directly. It was routed via Johann Heinrich von Bernstorff, the German Ambassador to the US. Although the British didn’t know it at the time, this was because the arrangement between the US State Department and the German Foreign Office was that they could send diplomatic communications down the main US cable to Washington but no further. At that point, the Germans would have to make their own arrangements for onward transmission.
Whatever the reasons, Hall realised that this presented an opportunity. Von Bernstorff would have to retransmit the message at the American end. The German Embassy, Room 40 knew, had a commercial relationship with Western Union in the United States, so this was likely how von Bernstorff would do it.
Room 40 also knew that he would also have to decrypt and then re-encrypt the message before doing so, as the Germans never used their own, high-level codes on commercial networks. Doing so risked opening them up too much to codebreaking efforts. Based on previous experience, the men posited that the whole process of receipt in New York, handover from the State Department to the Germans, decryption, re-encryption and transmission over Western Union would take about five days.
Hall realised this whole process offered an opportunity they could exploit. The Western Union message would be in a lower code, transcribed by the Germans themselves. If they could get hold of that, at the Mexican end, then they could claim this was the source instead.
The Mexican connection
Until now, Room 40 had generally ignored the Western Union traffic as a potential source of high-value intelligence. Any kind of operation across the Atlantic would have involved not just stepping on American toes but smashing a large boot down on them repeatedly. Given the perceived low value of the traffic, it simply wasn’t worth the risk.
Hall pointed out though that right now they didn’t need everything that Germany was sending over Western Union. They didn’t even need a tap on the line. They just needed a copy of this specific telegram. They knew who it was going to, who it was from and — roughly — when it was likely to be sent. They just needed someone who could get hold of a copy from the Western Union office in Mexico City, no questions asked.
Hall made discreet inquiries with the British Embassy in Mexico. They confirmed that they had a source in the Western Union office in Mexico City — a clerk who, for the right price, would occasionally lift telegrams for them from Western Union’s files. Hall told them what to watch out for and when, although he refused to tell them why. Nonetheless, they agreed that they would try.
It was an inspired idea. A few days later, courtesy of the British Embassy in Mexico, a copy of the telegram, lifted directly from the files of the Mexico City office of Western Union, was delivered to Captain Hall’s desk by the Foreign Office.
The ambassador
On 19th February 1917, Captain Hall found himself standing in the offices of the US Ambassador to Britain in the heart of London.
19 days before, on the exact day indicated in the Zimmermann Telegram had indicated, Germany had begun waging unrestricted submarine warfare in the Atlantic. It had caused outrage and the breaking of diplomatic relations between Germany and the United States. Yet the US had remained neutral.
On 5th February — two weeks after De Grey and Dilly had first decrypted it — ‘Blinker’ Hall finally informed the British Foreign Office that the Zimmermann Telegram existed.
As Hall expected, the Foreign Office demanded to know the source. Hall was able to present them with the Western Union telegram, describing — with a straight face — how the message had been a ‘lucky intercept’ in Mexico, that had fallen into the hands of the British Embassy. They’d suspected it was significant, so had passed it on to Room 40, where it had been decrypted.
This was actually a lie on both accounts. Whilst it was clearly the same telegram as the one in the original “high” code that they had broken, somewhat ironically the “lesser” code that von Bernstorff had used (Diplomatic Code 13040) was one which the British hadn’t previously bothered trying to break. Luckily, another of the Room 40 codebreakers had spotted that it was similar to another naval code that they had broken elsewhere, and this had led to a partial decryption. Enough, at least, to fill in the gaps left in Dilly’s work on the original interception and confirm beyond a doubt that they were the same message.
On 18th February 1917, the Foreign Office had discreetly informed the US Ambassador, Walter Hines Page of the telegram’s existence, but Page was naturally suspicious. Whatever the state of US / German relations, he found it hard to believe that such an incredible telegram existed, let alone that the British would somehow have managed to obtain a copy. He told his personal secretary, Edward Bell, that he wanted more proof. Only then would he present this information to President Wilson.
This was why Captain Hall was standing in front of Edward Bell in the US Embassy now. He had been dispatched by the Foreign Office to meet with Bell and satisfy the Ambassador’s demands. The two men chatted cordially and the Captain told Bell the Mexico story and offered up his copy of the Western Union telegram as evidence. Bell agreed that it was compelling, but he still wanted more.
“I want to see it decrypted. In person.” Bell told the Captain.
Captain Hall smiled and sent for Nigel De Grey.
The final bluff
De Grey arrived soon after, clutching his notes on Diplomatic Code 13040. Captain Hall introduced him to Edward Bell and, with a relaxed smile, told De Grey what he was to do — decrypt the telegram while Bell watched.
On his part, De Grey couldn’t understand why the Captain was so relaxed, because internally De Grey himself was screaming. Hall had made an uncharacteristic mistake — he seemed to have forgotten that they hadn’t solved the Mexican version of the telegram. They only had a partial decrypt, largely based off the naval code it had been a close match for. Worse, De Grey hadn’t even bothered to write down all of the keys they had discovered in his own notes. There hadn’t seemed to be much point once they’d done enough to fill in the gaps on the original.
As he began to decode the telegram, under Bell’s watchful eye, De Grey realised he was going to have to improvise.
“If I stopped and fetched another book,” De Grey said later, “he would suspect at once that we’d faked it up for his benefit. If I let him see that I was writing it down out of my head, he would not believe me. If he did not believe me, we should fail and lose the greatest opportunity ever presented to us. Several seconds of bloody sweat. Then I bluffed. I showed him all the groups when they had been written in my book and passed quickly over those that were not, writing the words into the copy of the telegram by heart.”
“Edward Bell, the most charming man, was thoroughly convinced — the more easily I think in that he wanted to be convinced anyhow and regarded the whole thing as black magic.”
On the 20th February 1917, Bell handed over Hall’s copy of the Zimmermann telegram to Ambassador Page, telling him he agreed it was genuine, and suggesting they get Western Union to confirm that it was genuine. By the end of the month, the company had done so and a copy of Room 40’s decrypted version was in the hands of the President. On the 28th February 1917, Wilson handed it over to the American press.
The result
The United States of America declared war on Germany on the 5th April 1917, just over a month after the Zimmermann telegram had been handed over to the US Government. It is possible that unrestricted submarine warfare would have been enough to tip the US into intervention, eventually. The Zimmermann telegram, however, almost certainly made that inevitable. Few documents, in the entire history of information warfare, can be said to have had such an impact world history.
For the men of Room 40, it was a spectacular triumph, albeit one that none of the key players could talk about for considerable time to come. Indeed so good was Captain Hall’s cover story that it remained, for a long time, the official version of events. This suited ‘Blinker’ very well indeed. The Admiralty continued to read US Diplomatic traffic right up to — and indeed beyond — the end of the First World War.
“He was a perfectly marvellous person” Edward Bell later said of Captain Hall, “but the coldest-hearted proposition that ever was — he’d eat a man’s heart and hand it back to him.”
Both Dilly and De Grey were happy to keep the secret. They were codebreakers, and accepted that public acknowledgement rarely came with the job.
One of ‘Dilly’s Girls’ would later recall that, having been told the real story from the man himself at Bletchley, she asked him if either he, or De Grey, had received any kind of recognition.
“Gosh no!” Dilly replied, with a laugh. “But I believe Nigel did get an official telling off for running in the corridor!”
Like what I write? Then help me do more of it. Back London Reconnections, my transport site on Patreon. Every little helps tell a story.
Want a thorough and detailed account of Room 40 and its impact? Then buy Inside Room 40 by Paul Gannon.
Update!!!!
To everyone who said they wanted to know more about Dilly and the ‘Dilly Girls’ in WW2 — if we reach our Patreon target, then I will write up the remarkable tale of how Dilly, the women of the ISK, Prince Philip, a golfing British Admiral and an amorous Italian Ambassador all played a part in the last, great naval battle in the history of warfare.


 Chat about Tulip on our Discord!
Chat about Tulip on our Discord!